Overview:

PQSecure™ Technologies, LLC employs experts in the field of quantum cryptanalysis and offers this as a service. Quantum cryptanalysis is the study and evaluation of cryptographic algorithms in the presence of a quantum enabled adversary. While quantum computers are relatively young and small today, it is expected that within a decade they will be large enough to have an impact on the cryptographic algorithms currently deployed from our local computers, to the cloud, and everywhere in between. Therefore, we need to study their effects and understand the quantum resource requirements so that we may be properly prepared.

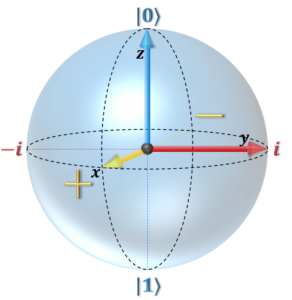
  • Bloch Sphere
The Bloch Sphere represents the different probabilities of a qubit.

The two main quantum resources are quantum bits, or qubits, and quantum gates. Qubits can take on any complex value between 0 and 1. That is a qubit, 𝑞, can be defined as |𝑞⟩ = 𝛼|0⟩ + 𝛽|1⟩ where 𝛼 and 𝛽 are complex probabilities, and |0⟩ and |1⟩ represent the computational basis states. This can be visually represented by the Bloch sphere on the right. Quantum gates can act on a single qubit at a time, or on multiple qubits at once, which is called quantum entanglement. Classical gates can be modeled with quantum gates, but there are a few quantum gates which cannot be classically modeled. One of these gates is the Hadamard gate which when applied to a basis state, puts the qubit into superposition.

Quantum Algorithms:

Even without access to quantum computers, we know how these computers could be used to break our current encryption schemes. Most notably there are two algorithms that can be used to attack cryptography. They are Shor’s quantum period finding algorithm which can only be used on public-key cryptography such as RSA and elliptic curve Diffie-Hellman (ECDH) and Grover’s quantum search algorithm which can be use against any algorithm such as block ciphers like AES or hash functions like SHA. While cryptographic community understands the broad effects of these algorithms the precise resource requirements are always being researched. The effects we know are:

  • Shor’s algorithm completely breaks current public-key algorithms like RSA, ECDH, ECDSA, etc., and thus these algorithms need to be replaced well before quantum computers are available.
  • Grover’s algorithm effectively cuts the key size in half, thus algorithms such as AES and SHA should double their key size to remain secure in the quantum age. 

Quantum Cryptanalysis Metrics:

The quantum resource requirements to attack cryptographic algorithms can be a bit large, so it is important to clearly detail the steps used to achieve the results and to publish the results in a standard that can be compared to in the future.  There are several candidates for these standards but in general the following are used:

  • Circuit Width – The maximum number of qubits required to be active at a single time step.
  • Circuit Depth – The number of time-steps required to run the circuit.
  • Depth x Width –A product of circuit width and circuit depth.
  • Number of Gates – Total number of quantum gates applied to the circuit.
  • Number of T-Gates – Total number of T-gates (more expensive to produce) applied to the circuit.
  • T–Depth – Number of time-steps in the circuit that implement a T-gate (takes longer to execute).
  • MAXDEPTH – A practical restriction placed on the circuit depth of either 240, 264, or 296.

Quantum Cryptanalysis Example (AES):

The Advances Encryption Standard (AES) was standardized by NIST in 2002 at the completion of their competition. It has since become the standard block cipher for securing sensitive information and AES-256 is even cited as used to secure classified government documents. Grover’s algorithm can be used to essentially cut this key size in half, thus giving AES-256 the security of AES-128. However, there is still some overhead here due to the way Grover’s algorithm must be applied. Reducing this overhead is one of the current goals of quantum cryptanalysis and many different techniques can still be leveraged.

Grover’s algorithm works in a way such that each time it is run, the result is more and more likely to be the AES encryption key. Thus, the same operations must be run many times to narrow down the result. One of the expensive internal operations of this attack is the AES multiplications which occur inside the AES Sbox, which works as sort of a mixing bowl. This AES multiplication happens many times per AES Sbox, which happen many times per AES circuit, which in turn happen many times in the Grover attack.

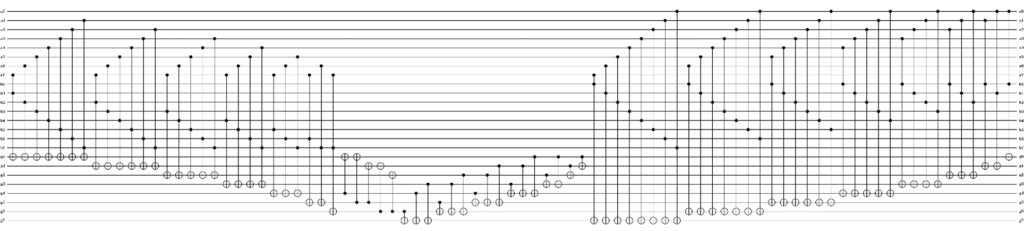
Example of AES modular multiplication of two 8-qubit numbers and storing the result on 8 additional qubits.

This operation is costly in terms of quantum gates and qubits, and thus working on ways to reduce this operation, as well as others is important work. Additionally, Grover’s algorithm is a very generic algorithm which can be tweaked and used in multiple ways to form an attack. It is also possible that a quantum algorithm that has yet been discovered could actually perform better, or some internal fault in AES could be exploited more efficiently. All of these are possible and areas where lots of research is still required.

What we Provide:

PQSecure’s industry experts stay up to date with the current work being done, the current researchers, and the known past and resent results in cryptanalysis. Using this as a starting point, we apply the best-known algorithms and attacks (combining classical and quantum adversaries) to the specific cryptographic algorithm to produce results that advance the current standard. Members of PQSecure have done work on symmetric and asymmetric (public-key) algorithms including classical and post-quantum solutions.